MoN10: Tenth Mathematics of Networks meeting, 16th September, Loughborough University
Alexander Hartmann (Oldenburg) - Large deviation properties of random graphs
The large-deviation properties of different types of random graphs are studied using numerical simulations.
First, distributions of the size of the largest
component, in particular the large-deviation tail,
are studied numerically for two graph ensembles,
for Erdős-Rényi random graphs
with finite connectivity and for two-dimensional bond percolation.
Probabilities as small as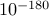 
are accessed
using an artificial finite-temperature (Boltzmann)
ensemble and applications of the Wang-Landau algorithm.
The distributions for the Erdős-Rényi ensemble
agree well with previously obtained analytical
results. The results for the percolation problem, where no analytical results
are available, are qualitatively similar, but the shapes of the distributions
are somehow different and the finite-size
corrections are sometimes much larger. Furthermore, for both problems,
a first-order phase transition
at low temperatures 
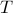within the artificial ensemble is found in the
percolating regime, respectively.
Second, the distributions of the diameter are presented. Here, partial analytic results are available from previous studies for Erdős-Rényi random graphs in the small connectivity region. The numerical results follow a Gumbel distribution and agree well with the analytics. For higher connectivities, where no analytic results are available, the simulation results show that the distributions are qualitatively different from the low connectivity region. This is also connected to a first-order phase transition within the associated finite-temperature ensemble.
Contact:
Keith Briggs
(
)
or
Richard G. Clegg (richard@richardclegg.org)